在看科普视频的时候学到了埃及分数和贪婪算法，这里用code实现一下。

埃及分数

古埃人使用的是象形文字，他们用这样的符号表示分数

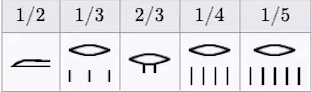
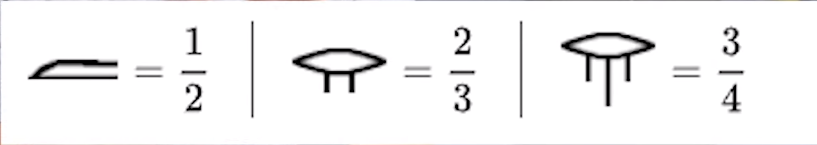
他们在圈圈下面画几个竖线代表几分之一，还有几个规定好的分数有特殊的符号，分数有无数多个，不可能给所有分数都画上符号，所以古埃及人把任意分数都表示为不同的单位分数的和，就是分子为1，分母为各不相同的正整数。任何正有理数都能表达成这一个形式。

例如：

$1=\frac{1}{2}+\frac{1}{3}+\frac{1}{6}$

1还可以表示为：

$1=\frac{1}{2}+\frac{1}{3}+\frac{1}{9}+\frac{1}{18}$

接下使用贪婪算法来生成任意一个正有理数的埃及分数形式。

贪婪算法

贪婪算法：将一项分数分解成若干项单分子分数后的项数最少，称为第一种好算法；最大的分母数值最小，称为第二种好算法。 例如：

${\displaystyle \frac{2}{7}=\frac{1}{4}+\frac{1}{28}}$。共2项，是第一种好算法，比${\displaystyle \frac{2}{7}=\frac{1}{5}+\frac{1}{20}+\frac{1}{28}}$的项数要少。

又例如，${\displaystyle \frac{5}{121}=\frac{1}{33}+\frac{1}{121}+\frac{1}{363}}\mathrm{比}{\displaystyle \frac{5}{121}=\frac{1}{25}+\frac{1}{759}+\frac{1}{208725}}$ 的最大分母要小，所以是第二种好算法。

找出仅小于${\displaystyle r=\frac{a}{b}}$的最大单位分数。这个分数的分母的计算方法是：即用${\displaystyle b}$除以${\displaystyle a}$，舍去余数，再加1。（如果没有余数，则${\displaystyle r}$已是单位分数。）
把${\displaystyle r}$减去单位分数，以这个新的、更小的${\displaystyle r}$重复步骤1。

例子：把${\displaystyle \frac{19}{20}}$转成单位分数。

${\displaystyle \lfloor 20÷19\rfloor =1}$，所以第1个单位分数是$\frac{1}{2}$；

${\displaystyle \frac{19}{20}-\frac{1}{2}=\frac{9}{20}}$；

${\displaystyle \lfloor 20÷9\rfloor =2}$，所以第2个单位分数是${\displaystyle \frac{1}{3}}$；

${\displaystyle \frac{9}{20}-\frac{1}{3}=\frac{7}{60}}$；

${\displaystyle \lfloor 60÷7\rfloor =8}$，所以第3个单位分数是${\displaystyle \frac{1}{9}}$；

${\displaystyle \frac{7}{60}-\frac{1}{9}=\frac{1}{180}}$已是单位分数。

所以结果是：
${\displaystyle \frac{19}{20}=\frac{1}{2}+\frac{1}{3}+\frac{1}{9}+\frac{1}{180}}$。

代码实现

# 寻找最大公约数
def _gcd(a, b):
    # Supports non-integers for backward compatibility.
    while b:
        a, b = b, a%b
    return a

# 约分
def ReduceFraction(numerator, denominator):
    if type(numerator) is int is type(denominator):
        g = _gcd(numerator, denominator)
        if denominator < 0:
            g = -g
        else:
            g = _gcd(numerator, denominator)
        numerator //= g
        denominator //= g
    return (numerator, denominator)

# 分数减法
def SubFraction(a, b):
    an, ad = a
    bn, bd = b
    numerator = an*bd - ad*bn
    denominator = ad * bd
    return ReduceFraction(numerator, denominator)

# 埃及分数生成器返回分母的list
def EgpytFraction(numerator=0, denominator=None, ret=[]):
    a = (denominator // numerator) + 1
    ret.append(a)
    t = SubFraction((numerator, denominator), (1, a))
    if t[0] == 1:
        ret.append(t[1])
        return ret
    return EgpytFraction(t[0], t[1], ret=ret)

EgpytFraction(5, 121, ret)
[25, 757, 763309, 873960180913, 1527612795642093418846225]

总结

埃及分数的表示不是唯一的，但应该有一个项数最少的表达式，我们把这个叫做最优的，但目前还没有一个算法可以求出最优的埃及分数。