4.机器学习
前四章的内容学习完毕,第五章讲了Octave这个软件的使用,类似于matlab,大学有过学习matlab经验所以这个学起来想对比较轻松,不论是在Ubuntu还是windows安装都很简单,这个的界面布局都和matlab基本一模一样。
虽然用python都可以实现,但Octave开源免费,比numpy更简单的实现算法,所以有必要学习一下。
其实关于Octave的东西并不想记录,和matlab一样,但为了这个博客的完整性还是简单的记录一下,我使用的是windows版的直接打开GUI就能使用了。
基本操作
%基本四则运算
>> 1+2
ans = 3
>> 6-1
ans = 5
>> 5*8
ans = 40
>> 1/5
ans = 0.20000
>> 3^6
ans = 729
%不等号是~而不是!
>> 1==2
ans = 0
>> 1~=2
ans = 1
%与 或 异或
>> 8 > 1 && 0
ans = 0
>> 9 > 1 || 0
ans = 1
>> xor(1, 0)
ans = 1
%如果你想分配一个变量,但不希望在屏幕上显示结果,你可以在命令后加一个分号,可以抑制打印输出,敲入回车后,不打印任何东西。
>> a = 3
a = 3
>> a = 3;
>> b = 'hello word';
>> b
b = hello word
%设置A等于圆周率π,如果我要打印该值,那么只需键入A像这样就打印出来了。
>> a = pi;
>> pi
ans = 3.1416
>> a
a = 3.1416
>> disp(sprintf('2 decimals: %0.12f', a))
2 decimals: 3.141592653590
这是一种,旧风格的C语言语法,对于之前就学过C语言的同学来说,你可以使用这种基本的语法来将结果打印到屏幕。
例如 sprintf命令的六个小数:0.6%f ,a,这应该打印π的6位小数形式。
也有一些控制输出长短格式的快捷命令:
>> format long
>> a
a = 3.14159265358979
>> format short
>> a
a = 3.1416
简单的运算符就是这些,重点是关于矩阵的
简单矩阵的创建
简单矩阵的创建
>> A = [1 2; 3 4; 5 6]
A =
1 2
3 4
5 6
>> A = [2 2;
3 3;
4 4]
A =
2 2
3 3
4 4
>> B = [1 2 3]
B =
1 2 3
>> B = [1; 2; 3]
B =
1
2
3
>>
这个集合V是一组值,从数值1开始,增量或说是步长为0.1,直到增加到2,按照这样的方法对向量V操作,可以得到一个行向量,这是一个1行11列的矩阵,其矩阵的元素是1 1.1 1.2 1.3,依此类推,直到数值2。
我也可以建立一个集合V并用命令“1:6”进行赋值,这样V就被赋值了1至6的六个整数。
>> v = 1:6
v =
1 2 3 4 5 6
这里还有一些其他的方法来生成矩阵
例如“ones(2,3)”,也可以用来生成矩阵:
>> ones(2,3)
ans =
1 1 1
1 1 1
元素都为2,两行三列的矩阵,就可以使用这个命令:
>> C = 2*ones(2,3)
C =
2 2 2
2 2 2
你可以把这个方法当成一个生成矩阵的快速方法。
w为一个一行三列的零矩阵,一行三列的A矩阵里的元素全部是零:
>> W = zeros(1,3)
W =
0 0 0
如果我对W进行赋值,用Rand命令建立一个一行三列的矩阵,因为使用了Rand命令,则其一行三列的元素均为随机值,如“rand(3, 3)”命令,这就生成了一个3×3的矩阵,并且其所有元素均为随机。
>> rand(3,3)
ans =
0.60790 0.22000 0.10036
0.61343 0.58981 0.17660
0.22697 0.88276 0.42049
>>
你知道什么是高斯随机变量,或者,你知道什么是正态分布的随机变量,你可以设置集合W,使其等于一个一行三列的
N矩阵,并且,来自三个值,一个平均值为0的高斯分布,方差或者等于1的标准偏差。
>> w = randn(1,3)
w =
-1.24688 1.87417 -0.70878
并用hist命令绘制直方图。
>> w = -9 + sqrt(10)*(randn(1, 10000));
>> hist(w)
>> hist(w,50)
绘制单位矩阵:
>> I = eye(6)
I =
Diagonal Matrix
1 0 0 0 0 0
0 1 0 0 0 0
0 0 1 0 0 0
0 0 0 1 0 0
0 0 0 0 1 0
0 0 0 0 0 1
对命令不清楚可以通过help命令查询
size函数
>> A = [1: 2; 3 4; 5 6]
A =
1 2
3 4
5 6
>> size(A) %输出[行数 列数]
ans =
3 2
>> size(A, 1) %行数
ans = 3
>> size(A, 2) %列数
ans = 2
>> length(A) %行数和列数中最大值
ans = 3
导入与导出数据
load 文件名
whos %将当前的变量都显示出来
clear A %将变量A删除
save hello.mat A; %将变量A存入hello.mat文件
save hello.txt A -ascii; %将A存为ascii
取矩阵中的值
>> A
A =
1 2
3 4
5 6
>> A(3,2) %矩阵A第三行第二列的数
ans = 6
>> A(2,:) %第二行的数
ans =
3 4
>> A(:,2) %第二列的数
ans =
2
4
6
>> A([1 3],:) %第一行和第三行的数
ans =
1 2
5 6
>> A(:,2) = [10;11;12] %修改第二列的数
A =
1 10
3 11
5 12
>> A = [A,[100;200;300]] %增加一列数据
A =
1 10 100
3 11 200
5 12 300
>> A(:) %修改为一列向量
ans =
1
3
5
10
11
12
100
200
300
拼接矩阵
>> A = [1 2; 3 4; 5 6]
A =
1 2
3 4
5 6
>> B = [11 12; 13 14; 15 16]
B =
11 12
13 14
15 16
>> C = [A B] %将矩阵A和B并列拼接
C =
1 2 11 12
3 4 13 14
5 6 15 16
>> C = [A;B] %加分号是将B矩阵拼接到A下面
C =
1 2
3 4
5 6
11 12
13 14
15 16
>>
矩阵计算
>> a = [1 2; 3 4; 5 6]
a =
1 2
3 4
5 6
>> B = [11 22; 33 44; 55 66]
B =
11 22
33 44
55 66
>> C = [1 1; 2 2]
C =
1 1
2 2
>> V = [1; 2; 3]
V =
1
2
3
>> A*C %矩阵相乘
ans =
5 5
11 11
17 17
>> A*B %相乘条件必须是A矩阵的列等于B矩阵的行,否则报错
error: operator *: nonconformant arguments (op1 is 3x2, op2 is 3x2)
>> A.*2 %矩阵中的每个元素都乘二
ans =
2 4
6 8
10 12
>> A.^2 %每个元素的平方
ans =
1 4
9 16
25 36
>> 1./V %每个元素的倒数
ans =
1.00000
0.50000
0.33333
>> V + ones(length(V), 1) %每个元素都加一
ans =
2
3
4
>> A' %A的转置
ans =
1 3 5
2 4 6
>>
矩阵的索引
>> a = [1 15 2 0.5]
a =
1.00000 15.00000 2.00000 0.50000
>> [val,ind] = max(a) % val 矩阵中的最大元素,ind 最大值的index
val = 15
ind = 2
>> val = max(A) %矩阵每列的最大值
val =
5 6
>> a < 3 %检查矩阵中比3小的元素,返回布尔型
ans =
1 0 1 1
>> find(a<3) %比3小的元素的位置
ans =
1 3 4
>> A = magic(3) %创建一个幻方 (行,列,对角线相加想等)
A =
8 1 6
3 5 7
4 9 2
>> [r c] = find(A>=7) % 符合A>=7元素的行列坐标
r =
1
3
2
c =
1
2
3
>> sum(a) %求所有元素的和
ans = 18.500
>> prod(A) %求每列的乘积
ans =
96 45 84
>> sum(A) %求每列的和
ans =
15 15 15
>> floor(a) %返回小于元素的最小整数
ans =
1 15 2 0
>> ceil(a) %返回大于元素的最大整数
ans =
1 15 2 1
>> max(rand(3), rand(3)) %比较两个矩阵返回最大值
ans =
0.65329 0.32803 0.23948
0.56627 0.37716 0.64170
0.17771 0.81867 0.73937
>> max(A, [], 1) %返回每一列的最大值
ans =
8 9 7
>> max(A, [], 2) %返回每一行的最大值
ans =
8
7
9
>> A = magic(9)
A =
47 58 69 80 1 12 23 34 45
57 68 79 9 11 22 33 44 46
67 78 8 10 21 32 43 54 56
77 7 18 20 31 42 53 55 66
6 17 19 30 41 52 63 65 76
16 27 29 40 51 62 64 75 5
26 28 39 50 61 72 74 4 15
36 38 49 60 71 73 3 14 25
37 48 59 70 81 2 13 24 35
>> sum(A,2) %行的和
ans =
369
369
369
369
369
369
369
369
369
>> sum(A,1) %列的和
ans =
369 369 369 369 369 369 369 369 369
>> sum(sum(A.* eye(9))) %对角线的和
ans = 369
>> pinv(A) %伪逆矩阵
画图
> t = [0 : 0.01 : 0.98];
>> y1 = sin(2*pi*4*t);
>> plot(t, y1,'r')
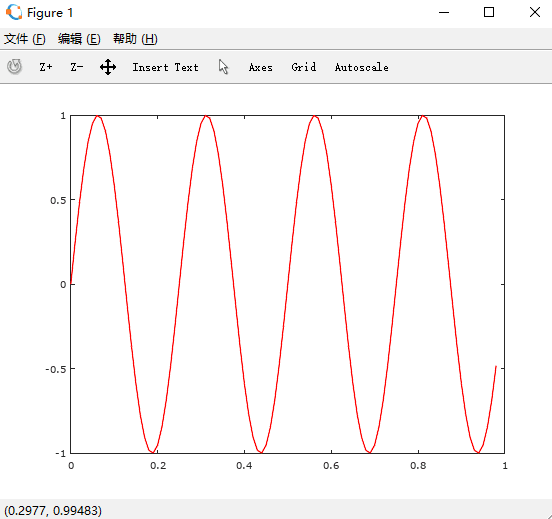
在一个画布上画两副如图
>> y1 = sin(2*pi*4*t);
>> y2 = cos(2*pi*4*t);
>> plot(t,y2)
>> hold on;
>> plot(t, y1,'r')
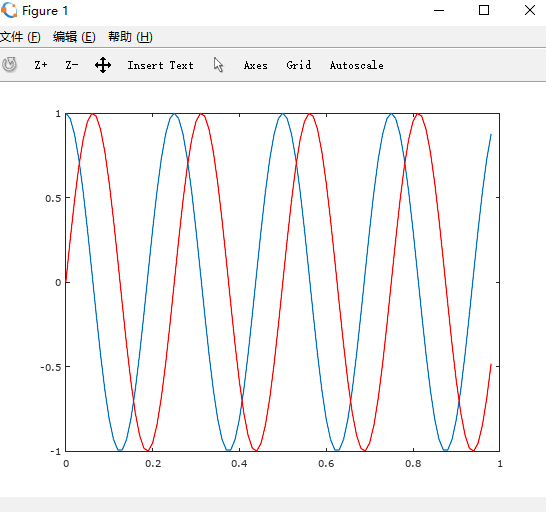
并列显示两个图
>> subplot(1,2,1)
>> plot(t,y1)
>> subplot(1,2,2)
>> plot(t,y2)
>> axis([0.5 1 -1 1])
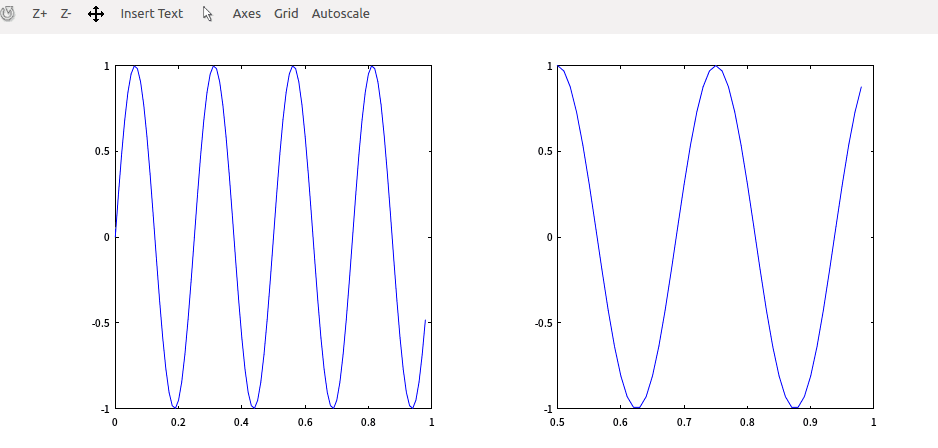
绘制矩阵
>> A = magic(5)
A =
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
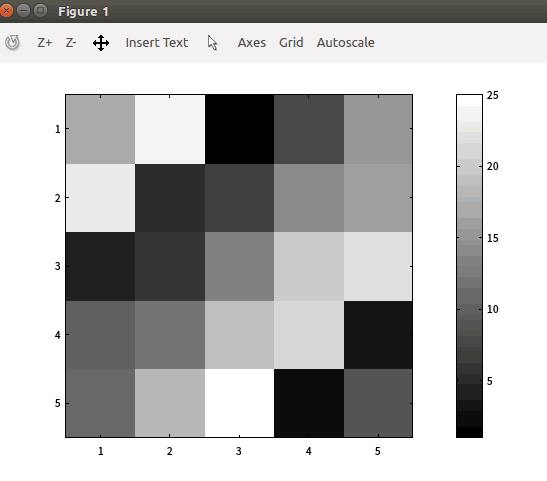
>> imagesc(A)
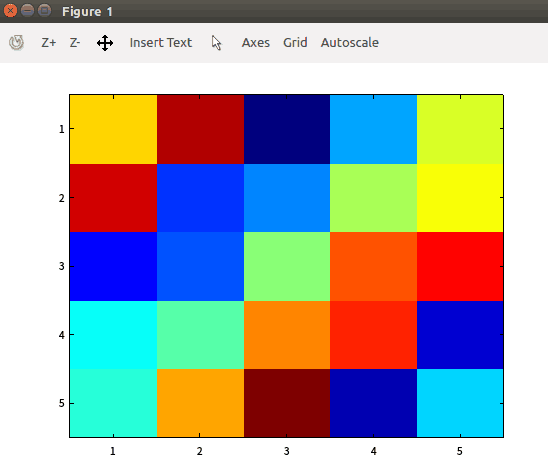
>> imagesc(A),colorbar,colormap gray;
控制语句
%for循环语句
>> v = zeros(1,10)
v =
0 0 0 0 0 0 0 0 0 0
>> for i = 1: 10
v(i) = 2^i;
end;
>> v
v =
2 4 8 16 32 64 128 256 512 1024
>>
%while语句
>> while i < 5,
v(i) = 100;
i = i+1
end
>> v
v =
2 4 8 16 32 64 128 256 512 1024
%if break语句
>> i = 1;
>> while true;
v(i) = 999;
i = i+1
if i==6,
break;
end
end
i = 2
i = 3
i = 4
i = 5
i = 6
>> v
v =
999 999 999 999 999 64 128 256 512 1024
>>
>> if v(1) == 1,
disp('The value is one!')
elseif v(1) == 2,
disp('The value is two!')
else
disp('The value is not one or two!')
end
The value is not one or two!
>>
定义函数
将函数定义写在文件中,并把文件名命名为‘函数名.m’,将文件放在当前路径下,或者用 addpath 将文件目录加入当前会话
本章学习结束