10. 机器学习实战
利用K-均值聚类算法对未标注数据分组
聚类是一种无监督的学习,它将相似的对象归到同一个簇中,它有点像全自动分类。聚类方法几乎可以应用于所有对象,簇内的对象越相似,聚类的效果越好。
K-means聚类算法,它可以发现k个不同的簇,且每个簇中心采用簇中所含值的均值计算而成。
簇识别(cluster identification)。簇识别给出聚类结果的含义。假定有一些数据,现在将相似数据归到一起,簇识别会告诉我们这些簇到底都是些什么。聚类与分类的最大不同在于,分类的目标事先已知,而聚类则不一样。因为其产生的结果与分类相同,而只是类别没有预先定义,聚类有时也被称为无监督分类(unsupervised classification)。
聚类分析试图将相似对象归入同一簇,将不相似对象归到不同簇。
K-均值聚类算法
优点:容易实现
缺点:可能收敛到局部最小值,在大规模数据集上收敛较慢
适用数据类型:数值型数据
K-means是发现给定数据集的k个簇的算法。簇的个数k是用户给定的,每一个簇通过其质心(centroid),即簇中所有点的中心来描述。
K-means算法的工作流程,首先随机确定k个初始点作为质心,然后将数据集的每个点分配到一个簇中,具体来讲,为每个点找距其最近的质心,并将其分配给该质心所对应的簇。这一步完成之后,每个簇的质心更新为该簇所有点的平均值。
伪代码如下:
创建k个点作为其实质心
当任意一个点的簇分配结果发生改变时
对数据集中的每个数据点
对每个质心
计算质心与数据点之间的距离
将数据点分配到距离其最近的簇
对每一个簇,计算簇中所有点的均值并将均值作为质心
K-means聚类的一般流程
- 收集数据
- 准备数据:需要数值型数据来计算距离,也可以将标称型数据映射为二值型数据再用于距离计算
- 分析数据
- 训练算法:不适用无监督学习,即无监督学习没有训练过程
- 测试算法:应用聚类算法,观察结果。可以使用量化的误差指标如误差平方和来评价算法的结果
- 使用算法:可以用于所希望的任何应用。通常情况下,簇质心可以代表整个簇的数据来做出决策
from numpy import *
def loadDataSet(fileName):
dataMat = []
fr = open(fileName)
for line in fr.readlines():
curLine = line.strip().split('\t')
fltLine = map(float, curLine)
fltLine = list(fltLine)
dataMat.append(fltLine)
return dataMat
def distEclud(vecA, vecB):
return sqrt(sum(power(vecA - vecB, 2)))
def randCent(dataSet, k):
n = shape(dataSet)[1]
centroids = mat(zeros((k, n)))
for j in range(n):
minJ = min(dataSet[:, j])
rangeJ = float(max(dataSet[:, j]) - minJ)
centroids[:, j] = minJ + rangeJ * random.rand(k, 1)
return centroids
distEclud()是计算两个向量的欧式距离
randCent()是为给定数据集构建一个包含k个随机质心的集合。随机质心必须要在整个数据集的边界之内,这可以找到数据集每一维的最小值和最大值来完成。然后随机生成0到1.0之间的随机数并通过取值范围和最小值,以便确保随机点在数据的边界之内。
datMat = mat(loadDataSet('MLiA_SourceCode/Ch10/testSet.txt'))
min(datMat[:, 0])
matrix(-5.379713)
min(datMat[:, 1])
matrix(-4.232586)
max(datMat[:, 1])
matrix(5.1904)
max(datMat[:, 0])
matrix(4.838138)
看下randCent()生成的值是否在max和min之间。
randCent(datMat, 2)
matrix([[-0.55362342, -1.69185255],
[ 0.43137443, -4.17749883]])
测试计算距离的函数
distEclud(datMat[0], datMat[1])
5.184632816681332
def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):
m = shape(dataSet)[0]
clusterAssment = mat(zeros((m, 2)))
centroids = createCent(dataSet, k)
clusterChanged = True
while clusterChanged:
clusterChanged = False
for i in range(m):
minDist = inf
minIndex = -1
for j in range(k): # 寻找最近的质心
distJI = distMeas(centroids[j, :], dataSet[i, :])
if distJI < minDist:
minDist = distJI
minIndex = j
if clusterAssment[i, 0] != minIndex:
clusterChanged = True
clusterAssment[i, :] = minIndex, minDist**2
print(centroids)
for cent in range(k):
ptsInClust = dataSet[nonzero(clusterAssment[:, 0].A == cent)[0]] # 更新质心的位置
centroids[cent, :] = mean(ptsInClust, axis=0)
return centroids, clusterAssment
centroids, clusterAssment = kMeans(datMat, 4)
centroids
[[ 4.01323567 3.90379869]
[-3.02008248 -3.35713241]
[ 0.85731381 0.6868651 ]
[ 0.45281866 -3.89960214]]
[[ 2.72275519 3.38230919]
[-3.53973889 -2.89384326]
[-0.92392975 2.12807596]
[ 2.42776071 -3.19858565]]
[[ 2.6265299 3.10868015]
[-3.53973889 -2.89384326]
[-2.31079352 2.63181095]
[ 2.7481024 -2.90572575]]
[[ 2.6265299 3.10868015]
[-3.53973889 -2.89384326]
[-2.46154315 2.78737555]
[ 2.65077367 -2.79019029]]
matrix([[ 2.6265299 , 3.10868015],
[-3.53973889, -2.89384326],
[-2.46154315, 2.78737555],
[ 2.65077367, -2.79019029]])
import matplotlib.pyplot as plt
def plotScatter(data):
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(data[:, 0].T.tolist()[0], data[:, 1].T.tolist()[0], 10, c='red')
ax.scatter(centroids[:, 0].T.tolist()[0], centroids[:, 1].T.tolist()[0], 50, marker='*')
plt.show()
plotScatter(datMat)
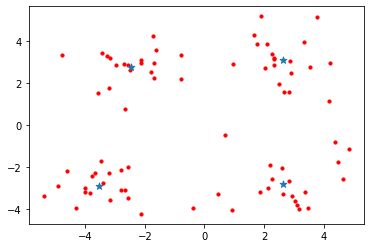
上面的结果得到四个质心。
使用后处理来提高聚类性能
利用点到质心的距离的平方值,来评价聚类质量。
另一种用于度量聚类效果的指标是SSE(sum of squared error,误差平方和),对应clusterAssment矩阵第一列之和。SSE值越小表示数据点越接近于他们的质心,聚类效果也越好。因为对误差取了平方,因此更加重视那些远离中心的点。
二分K-均值算法
为了克服K-均值算法收敛于局部最小值的问题,有人提出了一个称为二分K-均值的算法。该算法首先将所有点作为一个簇,然后将该簇一分为二。之后选择另一个簇进行划分,选择哪一个簇进行划分取决于对其划分是否可以最大程度降低SSE值。
伪代码如下:
将所有点看成一个簇
当簇数目小于k时
对每一个簇
计算总误差
在给定的簇上面进行K-均值聚类(k=2)
计算将该簇一分为二后的总误差
选择使得误差最小的那个簇进行划分操作
def biKmeans(dataSet, k, distMeas=distEclud):
m = shape(dataSet)[0]
clusterAssment = mat(zeros((m,2)))
centroid0 = mean(dataSet, axis=0).tolist()[0]
centList = [centroid0] # 创建一个初始簇
# 计算每个点到平均值的距离的平方
for j in range(m):
clusterAssment[j, 1] = distMeas(mat(centroid0), dataSet[j, :])**2
while (len(centList) < k):
lowestSSE = inf
for i in range(len(centList)):
ptsInCurrCluster = dataSet[nonzero(clusterAssment[:, 0].A==i)[0], :] # 获取当前数据集i中的数据点
centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas)
sseSplit = sum(splitClustAss[:, 1]) # 将SEE与当前的最小值进行比较
sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:, 0].A!=i)[0], 1])
print("sseSplit, and notSplit: ", sseSplit,sseNotSplit)
if (sseSplit + sseNotSplit) < lowestSSE:
bestCentToSplit = i
bestNewCents = centroidMat
bestClustAss = splitClustAss.copy()
lowestSSE = sseSplit + sseNotSplit
bestClustAss[nonzero(bestClustAss[:,0].A == 1)[0],0] = len(centList)
bestClustAss[nonzero(bestClustAss[:,0].A == 0)[0],0] = bestCentToSplit
print('the bestCentToSplit is: ',bestCentToSplit)
print('the len of bestClustAss is: ', len(bestClustAss))
centList[bestCentToSplit] = bestNewCents[0,:].tolist()[0] # 用两个最佳质心替换一个质心
centList.append(bestNewCents[1,:].tolist()[0])
clusterAssment[nonzero(clusterAssment[:,0].A == bestCentToSplit)[0],:]= bestClustAss # 更新簇的分配结果
return mat(centList), clusterAssment
datMat3 = mat(loadDataSet('MLiA_SourceCode/Ch10/testSet2.txt'))
centroids, clusterAssment = biKmeans(datMat3, 3)
centroids
[[ 0.94619158 -0.94117951]
[ 3.40877878 -0.10489155]]
[[-1.70351595 0.27408125]
[ 2.93386365 3.12782785]]
sseSplit, and notSplit: 541.2976292649145 0.0
the bestCentToSplit is: 0
the len of bestClustAss is: 60
[[-2.2226205 2.99958388]
[-2.07781041 4.61823253]]
[[-1.32962218 -0.58601139]
[-3.466158 4.32880371]]
[[-0.45965615 -2.7782156 ]
[-2.94737575 3.3263781 ]]
sseSplit, and notSplit: 67.2202000797829 39.52929868209309
[[3.31450775 4.54204866]
[2.24406919 1.79975326]]
[[3.26127644 3.86529411]
[2.66598045 2.52444636]]
[[3.43738162 3.905037 ]
[2.598185 2.60968842]]
sseSplit, and notSplit: 28.094839828868793 501.7683305828214
the bestCentToSplit is: 0
the len of bestClustAss is: 40
matrix([[-0.45965615, -2.7782156 ],
[ 2.93386365, 3.12782785],
[-2.94737575, 3.3263781 ]])
plotScatter(datMat3)
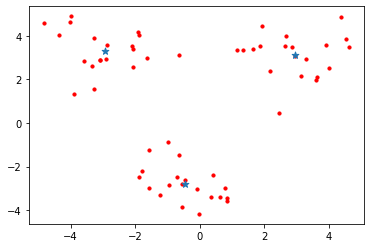
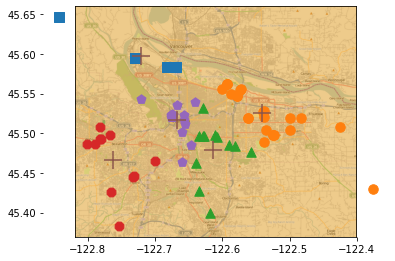
实例:对地图上的点进行聚类
def distSLC(vecA, vecB):#Spherical Law of Cosines
a = sin(vecA[0,1]*pi/180) * sin(vecB[0,1]*pi/180)
b = cos(vecA[0,1]*pi/180) * cos(vecB[0,1]*pi/180) * \
cos(pi * (vecB[0,0]-vecA[0,0]) /180)
return arccos(a + b)*6371.0 #pi is imported with numpy
import matplotlib
import matplotlib.pyplot as plt
def clusterClubs(numClust=5):
datList = []
for line in open('MLiA_SourceCode/Ch10/places.txt', 'r').readlines():
lineArr = line.split('\t')
datList.append([float(lineArr[4]), float(lineArr[3])])
datMat = mat(datList)
myCentroids, clustAssing = biKmeans(datMat, numClust, distMeas=distSLC)
fig = plt.figure()
rect=[0.1,0.1,0.8,0.8]
scatterMarkers=['s', 'o', '^', '8', 'p', \
'd', 'v', 'h', '>', '<']
axprops = dict(xticks=[], yticks=[])
ax0=fig.add_axes(rect, label='ax0', **axprops)
imgP = plt.imread('MLiA_SourceCode/Ch10/Portland.png')
ax0.imshow(imgP)
ax1=fig.add_axes(rect, label='ax1', frameon=False)
for i in range(numClust):
ptsInCurrCluster = datMat[nonzero(clustAssing[:,0].A==i)[0],:]
markerStyle = scatterMarkers[i % len(scatterMarkers)]
ax1.scatter(ptsInCurrCluster[:,0].flatten().A[0], ptsInCurrCluster[:,1].flatten().A[0], marker=markerStyle, s=90)
ax1.scatter(myCentroids[:,0].flatten().A[0], myCentroids[:,1].flatten().A[0], marker='+', s=300)
plt.show()
clusterClubs()
[[-122.56739405 45.62557076]
[-122.63486396 45.51036263]]
[[-122.842918 45.646831 ]
[-122.62856971 45.5103284 ]]
[[-122.76690133 45.612314 ]
[-122.62552961 45.50776091]]
[[-122.729442 45.58514429]
[-122.62063813 45.5040831 ]]
[[-122.74941346 45.545862 ]
[-122.60434434 45.50451707]]
[[-122.74823556 45.52585431]
[-122.59648847 45.50821685]]
[[-122.72797062 45.51642875]
[-122.58031918 45.51010827]]
[[-122.7142141 45.51492203]
[-122.56818551 45.5102949 ]]
[[-122.70981637 45.51478609]
[-122.56409551 45.51016235]]
sseSplit, and notSplit: 3073.8303715312386 0.0
the bestCentToSplit is: 0
the len of bestClustAss is: 69
[[-122.74578835 45.53605534]
[-122.83598851 45.6117388 ]]
[[-122.70552277 45.51052658]
[-122.842918 45.646831 ]]
sseSplit, and notSplit: 1351.7802960650447 1388.799845546737
[[-122.51444985 45.56152247]
[-122.6350006 45.49520857]]
[[-122.54062592 45.52653233]
[-122.607424 45.47994085]]
[[-122.54052872 45.52505652]
[-122.613193 45.47913283]]
sseSplit, and notSplit: 917.0774766267409 1685.0305259845018
the bestCentToSplit is: 1
the len of bestClustAss is: 37
[[-122.79462233 45.64436218]
[-122.77702826 45.44723276]]
[[-122.72070683 45.59796783]
[-122.70730319 45.49559031]]
sseSplit, and notSplit: 1047.9405733077342 917.0774766267409
[[-122.52922184 45.56204495]
[-122.41440445 45.48137939]]
[[-122.55266787 45.52993361]
[-122.4009285 45.46897 ]]
sseSplit, and notSplit: 361.2106086859341 1898.9745985610039
[[-122.63507677 45.48340811]
[-122.60541227 45.407053 ]]
[[-122.6105264 45.4923452]
[-122.626526 45.413071 ]]
sseSplit, and notSplit: 81.83580692942014 2388.16393003474
the bestCentToSplit is: 0
the len of bestClustAss is: 32
[[-122.82888364 45.5832033 ]
[-122.71555836 45.59441721]]
[[-122.842918 45.646831 ]
[-122.6962646 45.5881952]]
sseSplit, and notSplit: 24.09829508946755 1797.0816445068451
[[-122.52145964 45.55057242]
[-122.48348974 45.49208357]]
[[-122.57237273 45.5439008 ]
[-122.4927627 45.4967901 ]]
sseSplit, and notSplit: 307.68720928070644 1261.8846458842365
[[-122.60429789 45.49458255]
[-122.55803361 45.45874909]]
[[-122.61647322 45.49408122]
[-122.60335233 45.43428767]]
[[-122.6105264 45.4923452]
[-122.626526 45.413071 ]]
sseSplit, and notSplit: 81.83580692942014 1751.0739773579726
[[-122.78221469 45.49159997]
[-122.66948399 45.51952507]]
[[-122.7680632 45.4665528 ]
[-122.66932819 45.51373875]]
[[-122.761804 45.46639582]
[-122.66733593 45.5169996 ]]
sseSplit, and notSplit: 335.01842722575645 1085.0138820543707
the bestCentToSplit is: 3
the len of bestClustAss is: 26
总结
聚类是一种无监督学习方法。所谓无监督学习是指事先不知道要寻找的内容,即没有目标变量。聚类将数据点归到多个簇中,其中相似数据点处于同一簇,而不相似数据点处于不同簇中。聚类可以使用多种不同的方法来计算相似度。
一种广泛使用的聚类算法是K-均值算法,其中k是用户指定的要创建的簇的数目。K-均值聚类算法以k个随机质心开始。算法会计算每一个点到直线的距离。每个点会被分配到距其最近的簇质心,然后紧接着基于新分配到簇的点更新簇质心。重复以上过程数次,直到质心不再改变。
为获得更好的聚类效果,可以使用二分K-均值的聚类算法。二分K-均值算法首先将所有点作为一个簇,然后使用K-均值算法(k=2)对其划分。下一次迭代时,选择有最大误差的簇进行划分。该过程重复直到k个簇创建成功为止。
二分K-均值的聚类效果要好于K-均值算法。